No es raro encontrar gráficos como este. 👉
Se trata de una sala de cuidados intensivos donde hay 50 personas no vacunadas (en rojo) y 40 vacunadas (en verde). Gráficos de este tipo suelen acompañarse de un aviso como que el "44.4% de las internadas estaban vacunadas" o bien que "el 55.6% de las internadas en cuidados intensivos no estaban vacunadas", que es lo mismo. Una lectura simple nos dice que las no vacunadas son la mayoría en la sala de cuidados intensivos. Este tipo de información es muy requerido por todos, con la esperanza de que dé alguna información sobre la efectividad de las vacunas. Pero en realidad un gráfico así nada nos dice de la efectividad de una vacuna para prevenir este tipo de internaciones. Aun más, a partir de la llegada de la variante ómicron se incrementó la cantidad de gente que se internaba por una causa y se encuentra que también está infectada por covid. De este modo en algunos países como Escocia o Dinamarca las internaciones se dividen en pacientes internados "por covid" y pacientes con "covid". Pero sigamos:
Estas cifras de hospitalización, sin ser falsos, distorsionan la realidad y afectan a la racionalidad de nuestro juicio sobre la efectividad de las vacunas frente a la covid. Tienen dos grandes problemas: la información que ofrecen está mal “enmarcada” y la paradoja de Simpson.
El efecto marco (framework effect) es un sesgo cognitivo que modifica nuestras preferencias, haciéndolas menos racionales, según la forma en que nos es presentada. ("enmarcada") la información. No soy un experto en comunicación, pero supongo que es algo que siempre deben tener en cuenta en los grandes medios de comunicación. El concepto
fue introducido por los premios de Nobel de Economía Kahneman y Tversky en 1981 en un artículo que publicaron en Science.
Muy simplificadamente, a los participantes se les dio a elegir entre un hipotético tratamiento para 600 pacientes con una grave enfermedad que salvaría a 200 de ellos, frente a otro hipotético tratamiento con el que fallecerían 400. Aunque ambas alternativas son idénticas (en ambas 200 personas sobreviven y 400 fallecen), la mayoría de los participantes prefirieron el tratamiento que salvaba vidas, porque fue “enmarcado” o connotado positivamente.
Sin ser tan académicos creo que todos sabemos que la reacción de otros va a cambiar según la forma en que le presentemos la información. En el ejemplo gráfico uno puede decir que las no vacunadas se internan más que las vacunadas, pero también puede decir que un 44.4% de las internadas estaban vacunadas. Todo depende si lo quiero connotar positivamente. Pero en epidemiología sabemos que si no consideramos la procedencia de estas internaciones de poco nos vale.
Sigamos con el ejemplo: nuestra sala de UCI tiene 90 internaciones diarias, 40 en vacunadas (40*100/90 = 44,4 % de las internadas están vacunadas) y 50 en no vacunadas (50*100/90 = 55,6 % de las internadas no están vacunadas). Ahora sumemos otro dato, que es la vacunación en la misma región donde está nuestra sala de cuidados intensivos, ya que esta sala da cobertura a 5.5 millones de personas mayores de 12 años en nuestra comarca.
Si quisieramos tener una incidencia de las internadas en UCI sería de (90*100.000/5.500.000 =) 1,6 ingresadas por 100.000 personas mayores de 12 años/dia. Pero esta cifra conjunta de vacunadas y no vacunadas, que a veces se reporta en las estadísticas oficiales, no ofrece mucha información sobre el riesgo de ingreso en UCI de las vacunadas y las no vacunadas.
Agreguemos más datos. Asumamos que el
91 % de la población mayor de 12 años (5.5*0,91=5 millones) está vacunada,
mientras que el 9 % restante (500.000) no lo está. Con estados datos ya
podemos ofrecer una información mejor enmarcada (Figura 2): Los 500.000 no vacunados han generado 50 ingresos/semana en UCI, con una tasa de (50*100.000/500.000) 10 ingresos por 100.000 no vacunados a la semana. Los 5 millones de vacunados han generado 40 internaciones, con una tasa de (40*100.000/5.000.000) de 0,8 internaciones en UCI por 100.000 vacunados.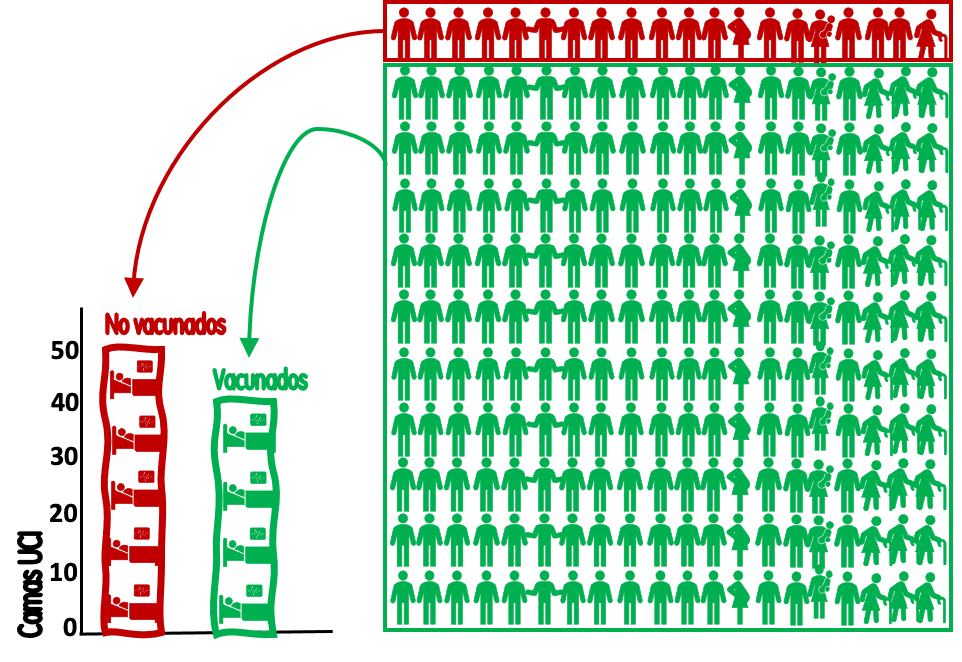
Sobre estas dos tasas poblacionales (en vacunadas y no vacunadas) yo puedo calcular un riesgo (en epidemiología le decimos riesgo a una probabilidad). En este caso será 10 / 0.8 = 12.5 veces más probable que una no vacunada se interne en comparación con los que sí se vacunaron. Esto es lo mismo a lo que se presenta en los estudios de caso control donde se expresa la probabilidad con un odd ( o chance), en este caso el "odd ratio" será el calculado 12.5.
El primero que hizo cálculos de este tipo fue un médico llamado John Snow, alrededor de 1848 en Londres, que tras analizar algunas bombas de agua concluyó que la causa del cólera estaba en el agua que tomaban las personas que vivian en Londres. No tuvo mucho éxito en su época, porque lo descubrió antes que los humanos supieramos las bacterias existian.
Estas tasas de incidencia poblacionales y separadas por grupos ya informan a vacunadas y a no vacunadas de su diferencia en riesgo de internarse en la UCI diariamente: 12,5 veces más en no vacunadas (que es lo mismo que decir que la probabilidad de internarse es de un 92.5% menor en vacunadas*) y ofrecen una información mejor “enmarcada” para la toma de decisiones que traslada confusamente la idea de que estos riesgos se repartían casi mitad y mitad. Estos datos, tasas poblacionales y riesgos relativos (y no la proporción de personas ingresadas), son los que importan para informar las preferencias racionales sobre la vacunación.
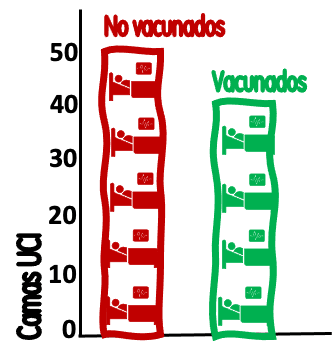
Recordemos que, al extremo, si el 100 % de los habitantes de la comarca estuvieran vacunadas, todos los ingresos en UCI procederían de esta población. La gran diferencia estaría en que los 500.000 previamente no vacunadas habrían producido solo 4 ingresos/semana (0,8/100.000; 12,5 veces menos que los 50 del ejemplo) y en la UCI solo habrían ingresado esa semana un total de 44 personas en lugar de 90 (Figura 3).
También podemos inferir que aunque las no vacunadas sean pocas en este ejemplo (el 9%) todavía el impacto en las internaciones graves puede ser grande. Y la idea es que las camas estén disponibles para otros problemas de salud, o mejor aun que estén disponibles y que no se ocupen.
Factores "confundidores" y paradoja de Simpson
El efecto "marco" no es el único problema que existe en ciencia a la hora de interpretar resultados. También existe una importante confusión (efectos "confundidores") por la mayor incidencia de covid grave en personas mayores de 65 años en relación a las más jóvenes y el hecho de que estas personas se hayan vacunado en mayor proporción que las de menor edad.
Dicho de otro modo: la edad es un "riesgo" (que en epidemiología quiere decir que incrementa la probabilidad) de padecer covid grave pero también de que se vacunen más.
En 1951, un matemático llamado Edward H. Simpson (la H es de Hugh no de Homero), describió una paradoja estadística que nos permite entender porque, en apareciencia, a veces las estadísticas parecen mostrar en internación más pacientes vacunados que no vacunados. Es importante que lo sepa, porque todas las estadísticas de los grupos antivacunas se basan en utilizar los datos de esta forma. Y es la forma en que en Argentina, el homéopata Eduardo Yahbes interpretó los datos del Ministerio de Salud en Agosto de 2021, concluyendo que el 90% de las muertes en Argentina ocurrían en vacunados. Poco importó que la afirmación fuera falsa, porque fue rápidamente difundida y aun todavía se cita como argumento. No siempre se trata de datos, sino también de cual es el relato que alguna gente quiere para reafirmar sus ideas preconcebidas.
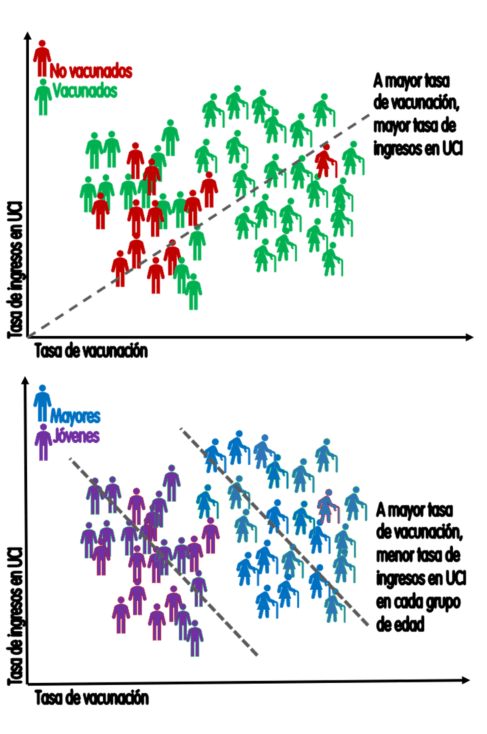
En el ejemplo de la figura, al estratificar por edad se invierte la tendencia y a mayor vacunación menor tasa de ingresos por covid dentro de cada grupo de edad. En otras palabras: las vacunadas tienen una mayor incidencia de casos graves no por ser vacunadas, sino por su mayor edad; pero dentro de cada grupo de edad las vacunadas tienen menor incidencia de casos graves que las no vacunadas.
Figura 4. Paradoja de Simpson: a más vacunadas más ingresos en población total, pero menos cuando se estratifica por edad. Cada cama representa 10 ingresos; cada figura humana representa 25.000 habitantes.
Lo que la paradoja de Simpson enseña a la hora de informar las preferencias sobre vacunación es que, si no se estratifica por edad, los casos graves en vacunadas estarán sobrerrepresentados porque hay una mayor proporción de personas mayores vacunadas y, a su vez, las personas mayores tienen un riesgo aumentado de desarrollar covid grave.
Como informar sobre la efectividad ahora
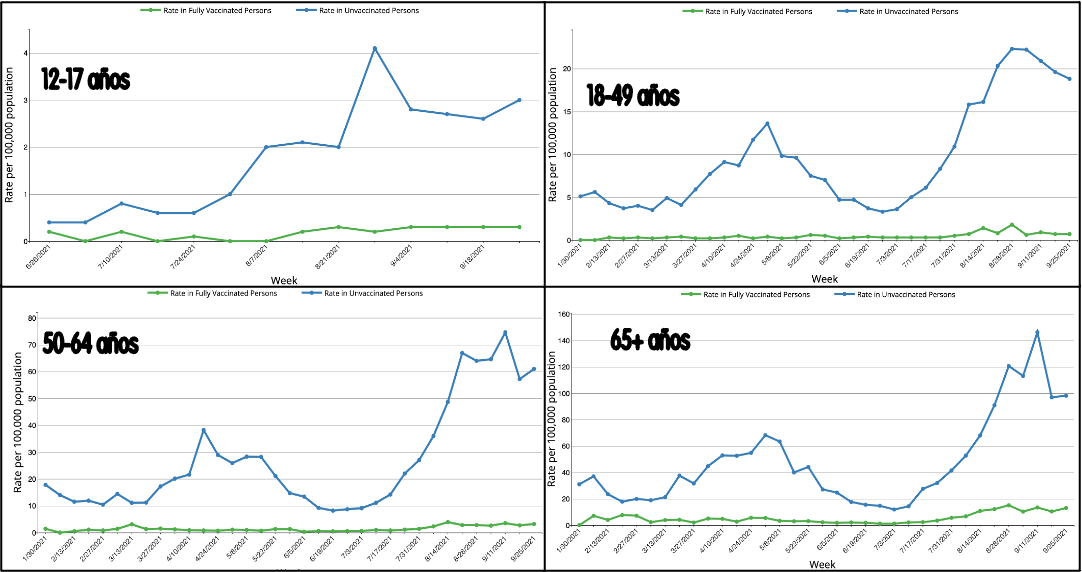
El hecho de que la mayor parte de la población esté vacunada obliga a cambiar la estrategia de comunicación. Ya que saber cuantos pacientes vacunados o no están internados no tiene mucho valor. La mejor manera es sin duda mostrando los gráficos por edades, en epidemiología llamamos a esto "estratificarlos". De esta manera se pueden "enmarcar" más adecuadamente, e incrementar las medidas no farmacológicas acorde al avance de la epidemia. Salvador Peiró con datos del CDC lo muestra en una gráfica que el hizo, y que le muestro aquí:
Se ve claramente que las tasas de internación en vacunadas (color verde) está muy por debajo de las tasas de internación en no vacunadas (en azul). Muchos países pueden mostrar esto, desafortunadamente no es el caso de Argentina. Pero ayuda a interpretar otras estadísticas como los casos o la mortalidad también.
Seguramente esto no cambia la disposición de nadie para vacunarse o no, pero si puede ayudar a que podamos interpretar mejor los gráficos y a pedir gráficos que tengan más información. Y sobre todo interpretarlos por uno mismo, ya que a diario veo gráficos que son "malinterpretados" con poca ciencia y menos conciencia.
Los datos constituyen una parte del conocimiento, la otra es la forma en que esos datos son enmarcadas, eso es el relato que se construye a partir de estos datos. Pero la mente no funciona así. En general se construye un relato y se realzan los datos que coinciden con nuestra forma de ver la realidad. En ciencia se piensa igual, pero si se ejerce honestamente existe la posibilidad de cambiar de opinión ante los nuevos datos. En el caso específico de vacunarse o no también inciden otras cuestiones, como el riesgo. Aun así los humanos no siempre valoramos los riesgos o probabilidades adecuadamente, si así fuera seguramente la lotería no sería un impuesto a la ignorancia.
Artículos relacionados
- Estadística para redes sociales
- El informe original de Salvador Peiró se puede leer aquí.
- Un impuesto a la ignorancia (Adrián Paenza)
- La paradoja de Simpson (Adrián Paenza)
* Se puede transformar un odd en probabilidad mediante la fórmula
Odd/=Odds + 1, en este caso seria 12.5 / 12.5 + 1 = 0.925, que es lo
mismo que decir 92.5%.

Brillante!
ResponderBorrarExcelente
Borrar