La biblioteca de Springfield

31 de enero de 2018

Intervalos de confianza

En una curva normal, o de Gauss, el porcentaje de la población que abarca el primer desvio standard, hacia ambos lados de la media es del 68%, por lo que si quisieramos expresar solo a este el intervalo de confianza seria expresado en un estudio clínico como IC68. Los resultados, en los estudios clinicos, suelen reportarse con la media, o promedio, de la muestra estudiada y su dispersión. Tomemos un ejemplo: tras dos dosis de una vacuna en Estados Unidos, se encontró que la hospitalización se redujo un 93% CI95 83%-97%. Esto significa que la reducción de internaciones tuvo una media del 93%, pero para el 95% de la población estudiada podia ser tan cierto una reducción tan baja como el 83% o tan alta como un 97%. A veces nos sirve tener un estimador puntual, otras nos interesa la variabilidad, pero casi siempre las dos dos estimaciones.

Asi es como suelen reportarse los resultados en los estudios clínicos que leemos en las revistas médicas.

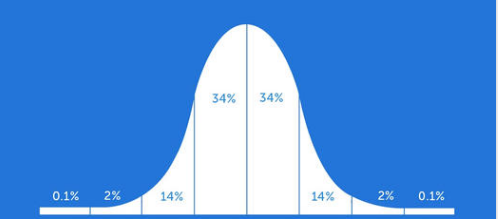
La media es entonces un estimador puntual y los intervalos de confianza representan la dispersión o variabilidad.

En una de distribución de Gauss puede verse claramente que al elegir un alfa (probabilidad de que un valor no esté dentro del intervalo de confianza) del 5%, caerá en la curva entre 1,96 y -1,96 desvio standard respecto a la media. Algunos estudios, para aportar mayor precisión, reportan un mayor nivel de confianza, por ejemplo al 99%.

A medida que aumente la población que fue estudiada, la amplitud del intervalo de confianza será menor, pero de mayor precisión. Esto se puede demostrar con una simple calculadora que toma en cuenta la población, la media y el desvio standard.

Es por ello que cuando mayor es el número de personas en el estudio, menor es la amplitud o rango de nuestro intervalo de confianza, y por ende más preciso.

Graficamente es enseñado con una curva de Gauss, pero también se puede encontrar en un box-plot o simplemente con lineas horizontales atravesando un punto. Donde el punto representa a la media y los extremos de la línea representan los intervalos inferior y superior.

Estos últimos gráficos suelen ser útiles para representar a múltiples estudios en un mismo gráfico, por ejemplo en un metanálisis, que representa a esto en un tipo de gráfico que llamamos Forest Plot.

En el gráfico se explica más claramente como interpretar visualmente los resultados, generalmente el efecto nulo se señala como 1 (esto significa que la probabilidad que un evento ocurra o no ocurra es la misma, o 1 versus 1, es decir el 50% de las veces, el peor escenario para las estadísticas). Si se trata de vacunas y lo que medimos es la disminución de la mortalidad, lo que esperamos es que la media y sus intervalos de confianza estén a la izquierda de ese uno. Pero si midieramos el incremento de los anticuerpos, lo que queremos es que este a la derecha. Si los intervalos de confianza atraviesan el efecto nulo diremos que el efecto encontrado no fue clínicamente significativo, dicho de otro modo, no se pudo demostrar diferencia entre el tratamiento en cuestión y el placebo.

Más todavia, si comparo dos tratamientos entre si, y los intervalos de confianza se solapan, o se superponen, esto indicaria que no hay diferencia entre los dos. Tal como se observa con las dos curvas de Gauss en el gráfico.

Los resultados para la mayoria de los fármacos eficaces los riesgos relativos suelen estar entre 1 y 2. Pero como a veces nos encontramos estudios contradictorios, preferimos los metanálisis que contienen a varios estudios originales, y los resultados suelen expresarse como el rombo del gráfico, donde los extremos del mismo marca los intervalos de confianza, el tamaño suele expresar el tamaño poblacional y la ubicación en relación al efecto nulo nos indica claramente cual fue la respuesta obtenida.