El efecto Dunning-Kruger

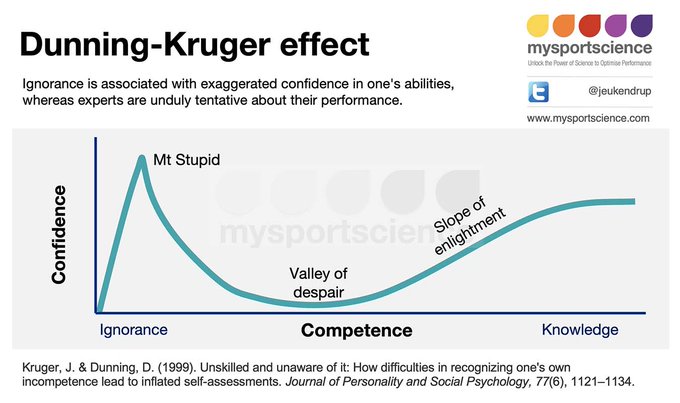
 ¿Ha oído hablar del 'efecto Dunning-Kruger'? Es la tendencia (aparente) de las personas no calificadas a sobrestimar su competencia y también la tendencia de los más calificados a subestimar sus competencias. Descubierto en 1999 por los psicólogos Justin Kruger y David Dunning , el efecto se ha hecho famoso desde entonces.

Y puedes ver por qué.

Es el tipo de idea que es demasiado buena para  no ser cierta. Todo el mundo 'sabe' que los idiotas tienden a no ser conscientes de su propia idiotez. O como dice John Cleese :

Si eres muy, muy estúpido, ¿Cómo es posible que te des cuenta de que eres muy, muy estúpido?

Por supuesto, los psicólogos han tenido cuidado de asegurarse de que la evidencia se reproduzca. Pero, por supuesto, cada vez que lo busca, el efecto Dunning-Kruger salta de los datos. Así que parecería que todo va sobre bases sólidas.

Excepto que hay un problema.

El efecto Dunning-Kruger también surge de datos en los que no debería . Por ejemplo, si elabora cuidadosamente datos aleatorios para que no contengan un efecto Dunning-Kruger, seguirá encontrando el efecto . La razón resulta vergonzosamente simple: el efecto Dunning-Kruger no tiene nada que ver con la psicología humana. Es un artefacto estadístico, un impresionante ejemplo de autocorrelación.

¿Qué es la autocorrelación?

La autocorrelación ocurre cuando correlaciona una variable consigo misma. Por ejemplo, si mido la altura de 10 personas, encontraré que la altura de cada persona se correlaciona perfectamente consigo misma. Si esto suena como un razonamiento circular, es porque lo es. La autocorrelación es el equivalente estadístico de afirmar que 5 = 5.

Cuando se enmarca de esta manera, la idea de autocorrelación suena absurda. Ningún científico competente correlacionaría una variable consigo misma. Y eso es cierto para la forma pura de autocorrelación. Pero, ¿qué pasa si una variable se mezcla en ambos lados de una ecuación, donde se olvida? Por esa causa, la autocorrelación es más difícil de detectar.

Aquí hay un ejemplo. Supongamos que estoy trabajando con dos variables, x e y . Encuentro que estas variables no están correlacionadas en absoluto, como se muestra en el panel izquierdo de la Figura 1. Hasta aquí todo bien.

Figura 1: Generación de autocorrelación. El panel izquierdo traza las variables aleatorias x e y , que no están correlacionadas. El panel derecho muestra cómo esta no correlación puede transformarse en una autocorrelación. Definimos una variable llamada z , que está fuertemente correlacionada con x . El problema es que z resulta ser la suma x + y . Entonces estamos correlacionando x consigo mismo. La variable y añade ruido estadístico.

A continuación, empiezo a jugar con los datos. Después de un poco de manipulación, se me ocurre una cantidad que llamo z . Guardo mi trabajo y me olvido de él. Meses después, mi colega revisa mi conjunto de datos y descubre que z se correlaciona fuertemente con x (Figura 1 , derecha). ¡Hemos descubierto algo interesante!

De hecho, hemos descubierto la autocorrelación. Sin el conocimiento de mi colega, he definido la variable z para que sea la suma de x + y . Como resultado, cuando correlacionamos z con x , en realidad estamos correlacionando x consigo mismo. (La variable y viene por el camino, proporcionando ruido estadístico). Así es como ocurre la autocorrelación, olvidando que tiene la misma variable en ambos lados de una correlación, en el gráfico entonces la variable está presente en ambos ejes.

El efecto Dunning-Kruger

Ahora que comprende la autocorrelación, hablemos del efecto Dunning-Kruger. Al igual que el ejemplo de la Figura 1, el efecto Dunning-Kruger equivale a una autocorrelación. Pero en lugar de acechar dentro de una variable re etiquetada, la autocorrelación de Dunning-Kruger se esconde debajo de un gráfico engañoso. 

Veamos:

En 1999, Dunning y Kruger informaron los resultados de un experimento simple. Consiguieron un grupo de personas para completar una prueba de habilidades. Luego le pidieron a cada persona que evaluara su propia habilidad. Lo que Dunning y Kruger (pensaron que) encontraron fue que las personas que obtuvieron malos resultados en la prueba de habilidades también tendían a sobrestimar su capacidad. Ese es el 'efecto Dunning-Kruger'.

Dunning y Kruger visualizaron sus resultados como se muestra en la Figura 2 . Es un gráfico simple que llama la atención sobre la diferencia entre dos curvas. En el eje horizontal, Dunning y Kruger han colocado a las personas en cuatro grupos (cuartilos) según sus puntajes en las pruebas. En el gráfico, las dos líneas muestran los resultados dentro de cada grupo. La línea gris indica los resultados promedio de las personas en la prueba de habilidades. La línea negra indica su 'capacidad percibida' promedio. Claramente, las personas que obtuvieron una puntuación baja en la prueba de habilidades tienen un exceso de confianza en sus habilidades. (O eso parece).

Figura 2: El gráfico de Dunning-Kruger. De Dunning y Kruger (1999) . Esta figura muestra cómo Dunning y Kruger informaron sus hallazgos originales. Dunning y Kruger dieron una prueba de habilidades a los individuos y también le pidieron a cada persona que estimara su habilidad. Dunning y Kruger luego colocaron a las personas en cuatro grupos según sus puntajes de prueba clasificados. Esta figura contrasta el percentil (promedio) de la 'puntuación real de la prueba' dentro de cada grupo (línea gris) con el percentil (promedio) de la 'capacidad percibida'. El 'efecto' Dunning-Kruger es la diferencia entre las dos curvas: el hecho (aparente) de que las personas no calificadas sobrestiman su capacidad.

Por sí solo, el gráfico de Dunning-Kruger parece convincente. Agregue el hecho de que Dunning y Kruger son excelentes escritores, y tiene la receta para un artículo exitoso. En ese sentido, te recomiendo que leas su artículo, porque nos recuerda que no es lo mismo buena retórica que buena ciencia.

Deconstruyendo Dunning-Kruger

Ahora que ha visto el gráfico de Dunning-Kruger, mostremos cómo oculta la autocorrelación. Para aclarar las cosas, comentaré los gráficos a medida que avanzamos.

Comenzaremos con el eje horizontal. En el gráfico de Dunning-Kruger, el eje horizontal es "categórico", lo que significa que muestra "categorías" en lugar de valores numéricos. Por supuesto, no hay nada de malo en trazar categorías. Pero en este caso, las categorías son en realidad numéricas. Dunning y Kruger toman los puntajes de las pruebas de las personas y las colocan en 4 grupos clasificados. (Los estadísticos llaman a estos grupos 'cuartilos').

Lo que significa esta clasificación es que el eje horizontal traza efectivamente la puntuación de la prueba. Llamemos a esta puntuación x .

Figura 3: Deconstrucción del gráfico de Dunning-Kruger. En el gráfico de Dunning-Kruger, el eje horizontal clasifica la "puntuación real de la prueba", que llamaré x .

A continuación, observemos el eje vertical, que está marcado como 'percentil'. Lo que esto significa es que en lugar de trazar los puntajes reales de las pruebas, Dunning y Kruger trazan la clasificación del puntaje en una escala de 100 puntos. 

Ahora veamos las curvas. La línea etiquetada como 'puntuación real de la prueba' traza el percentil promedio de la puntuación de la prueba de cada cuartilo. Las cosas parecen estar bien, hasta que nos damos cuenta de que Dunning y Kruger esencialmente están trazando el puntaje de la prueba ( x ) contra sí mismo. Notando este hecho, volvamos a etiquetar la línea gris. Grafica efectivamente x contra  x .

Figura 3: Deconstrucción del gráfico de Dunning-Kruger. En el gráfico de Dunning-Kruger, la línea marcada como "puntuación real de la prueba" representa la puntuación de la prueba ( x ) contra sí misma. En mi notación, eso es x contra  x .

Continuando, veamos la línea etiquetada como "capacidad percibida". Esta línea mide el percentil promedio de la autoevaluación de cada grupo. Llamemos a esta autoevaluación y . Si recordamos que hemos etiquetado la 'puntuación real de la prueba' como x , vemos que la línea negra representa y frente  a x .

Figura 3: Deconstrucción del gráfico de Dunning-Kruger. En el gráfico de Dunning-Kruger, la "capacidad percibida" del mercado de líneas representa la "capacidad percibida" y frente a la puntuación real de la prueba x .

Hasta ahora, nada salta a la vista como algo obviamente incorrecto. Sí, es un poco raro graficar x contra  x . Pero Dunning y Kruger no afirman que esta línea por sí sola sea importante. Lo importante es la diferencia entre las dos líneas ("capacidad percibida" frente a "puntuación real de la prueba"). Es en esta diferencia donde aparece la autocorrelación.

En términos matemáticos, una 'diferencia' significa 'restar'. Entonces, al mostrarnos dos líneas divergentes, Dunning y Kruger nos piden (implícitamente) que restemos una de la otra: tomemos la 'capacidad percibida' y restemos la 'puntuación real de la prueba'. En mi notación, eso corresponde a y – x .

Figura 3: Deconstrucción del gráfico de Dunning-Kruger. Para interpretar el gráfico de Dunning-Kruger, observamos (implícitamente) la diferencia entre las dos curvas. Eso corresponde a tomar la 'capacidad percibida' y restarle la 'puntuación real de la prueba'. En mi notación, esa diferencia es y – x (indicada por la flecha de dos puntas). Cuando juzgamos esta diferencia como una función del eje horizontal, implícitamente estamos comparando y – x con x . Dado que x está a ambos lados de la comparación, el resultado será una autocorrelación.

Restar y – x parece estar bien, hasta que nos damos cuenta de que se supone que debemos interpretar esta diferencia como una función del eje horizontal. Pero el eje horizontal traza la puntuación de la prueba x . Entonces se nos pide (implícitamente) que comparemos y – x con x :

$$\displaystyle (y - x) \sim x

¿Ves el problema? Estamos comparando x con la versión negativa de sí mismo . Esa es la autocorrelación de los libros de texto. Significa que podemos arrojar números aleatorios en x e y , números que posiblemente no podrían contener el efecto Dunning-Kruger, y sin embargo, en el otro extremo, el efecto seguirá emergiendo.

Réplica de Dunning-Kruger

Alguien escribió lo anterior, pero aun así no estaba convencido de sus argumentos, así que decidió usar datos reales. Solo usando datos reales puedo entender el problema con el efecto Dunning-Kruger. Veamos que sucedió.

Supongamos que somos psicólogos que reciben una gran subvención para replicar el experimento de Dunning-Kruger. Reclutamos a 1000 personas, les damos a cada una una prueba de habilidades y les pedimos que informen una autoevaluación. Cuando tenemos los resultados, echamos un vistazo a los datos.

Cuando graficamos el puntaje de la prueba de los individuos contra su autoevaluación, los datos parecen completamente aleatorios. La figura 7 muestra el patrón aleatorio. Parece que las personas de todas las habilidades son igualmente terribles para predecir su habilidad. No hay indicios de un efecto Dunning-Kruger.

Figura 7: una replicación fallida. Esta figura muestra los resultados de un experimento mental en el que intentamos replicar el efecto Dunning-Kruger. Hacemos que 1000 personas realicen una prueba de habilidades y estimen su propia capacidad. Aquí, trazamos los datos sin procesar. Cada punto representa el resultado de un individuo, con 'puntaje de prueba real' en el eje horizontal y 'autoevaluación' en el eje vertical. No hay indicios de un efecto Dunning-Kruger.

Después de mirar nuestros datos sin procesar, nos preocupa que hayamos hecho algo mal. Muchos otros investigadores han replicado el efecto Dunning-Kruger. ¿Cometimos un error en nuestro experimento?

Lamentablemente, no podemos recopilar más datos. (Nos hemos quedado sin dinero.) Pero podemos jugar con el análisis. Un colega sugiere que, en lugar de graficar los datos sin procesar, calculemos el "error de autoevaluación" de cada persona. Este error es la diferencia entre la autoevaluación de una persona y su puntaje en la prueba. ¿Quizás este error de evaluación se relaciona con el puntaje real de la prueba?

Hacemos los números y, para nuestro asombro, encontramos un efecto enorme. La figura 8 muestra los resultados. Parece que las personas no calificadas tienen un exceso de confianza, mientras que las personas calificadas son demasiado modestas.

(Nuestros técnicos de laboratorio señalan que la correlación es sorprendentemente estrecha, casi como si los números se hubieran elegido a mano. Pero dejamos de lado esta observación y seguimos adelante).

Figura 8: ¿Quizás el experimento fue exitoso? Usando los datos sin procesar de la Figura 7 , esta figura calcula el 'error de autoevaluación': la diferencia entre la autoevaluación de un individuo y su puntaje real en la prueba. Este error de evaluación (eje vertical) se correlaciona fuertemente con el eje (horizontal) de la puntuación real de la prueba.

Animados por nuestro éxito en la Figura 8, decidimos que los resultados pueden no ser "malos" después de todo. Entonces arrojamos los datos en el gráfico de Dunning-Kruger para ver qué sucede. Descubrimos que, a pesar de nuestras dudas sobre los datos, el efecto Dunning-Kruger estuvo presente todo el tiempo. De hecho, como muestra la Figura 9 , nuestro efecto es incluso mayor que el original (de la Figura 2 ).

Figura 9: Recuperación de Dunning y Kruger. A pesar de la aparente falta de efecto en nuestros datos sin procesar (Figura 8 ), cuando conectamos estos datos en el gráfico de Dunning-Kruger, obtenemos un efecto masivo. Las personas que no están calificadas sobrestiman sus habilidades. Y las personas hábiles son demasiado modestas.

Las cosas se desmoronan

Satisfechos con nuestra replicación exitosa, comenzamos a escribir nuestros resultados. Entonces las cosas se desmoronan. Lleno de culpa, nuestro curador de datos se sincera: perdió los datos de nuestro experimento y, en un ataque de pánico, los reemplazó con números aleatorios . Nuestros resultados, confiesa, se basan en ruido estadístico.

Devastados, volvemos a nuestros datos para dar sentido a lo que salió mal. Si hemos estado trabajando con números aleatorios, ¿cómo podríamos haber replicado el efecto Dunning-Kruger? Para averiguar qué pasó, dejamos de fingir que estamos trabajando con datos psicológicos. Reetiquetamos nuestros gráficos en términos de variables abstractas x e y . Al hacerlo, descubrimos que nuestro "efecto" aparente es en realidad una autocorrelación.

La figura 10 lo desglosa. Nuestro conjunto de datos se compone de ruido estadístico: dos variables aleatorias, x e y , que no tienen ninguna relación (Figura 10 A). Cuando calculamos el 'error de autoevaluación', tomamos la diferencia entre y y x . Como era de esperar, encontramos que esta diferencia se correlaciona con x (Figura 10 B). Pero eso es porque x se autocorrelaciona consigo mismo. Finalmente, desglosamos el gráfico de Dunning-Kruger y nos damos cuenta de que también se basa en la autocorrelación (Figura 10 C). Nos pide que interpretemos la diferencia entre y y x como una función de x . Es la autocorrelación del panel B, envuelta en un barniz más engañoso.

Figura 10: Abandonando la pretensión psicológica. Esta figura repite el análisis que se muestra en las Figuras 7 a 9, pero deja de lado la pretensión de que estamos tratando con la psicología humana. Estamos trabajando con variables aleatorias x e y que se extraen de una distribución uniforme. El panel A muestra que las variables no están correlacionadas en absoluto. El panel B muestra que cuando graficamos y – x contra x , obtenemos una fuerte correlación. Pero eso es porque hemos correlacionado x consigo mismo. En el panel C, ingresamos estas variables en el gráfico de Dunning-Kruger. Nuevamente, el efecto aparente equivale a la autocorrelación: interpretar y – x como una función de x.

El objetivo de esta historia es ilustrar que el efecto Dunning-Kruger no tiene nada que ver con la psicología humana. Es un artefacto estadístico, un ejemplo de autocorrelación que se esconde a plena vista.

Lo interesante es cuánto tiempo les tomó a los investigadores darse cuenta de la falla en el análisis de Dunning y Kruger. Dunning y Kruger publicaron sus resultados en 1999. Pero el error tardó hasta 2016 en comprenderse por completo. Edward Nuhfer y sus colegas fueron los primeros en desacreditar exhaustivamente el efecto Dunning-Kruger. (Consulte sus artículos conjuntos en 2016 y 2017 ). En 2020, Gilles Gignac y Marcin Zajenkowski publicaron una crítica similar .

Una vez que lee estas críticas, se vuelve dolorosamente obvio que el efecto Dunning-Kruger es un artefacto estadístico. Pero hasta la fecha, muy pocas personas conocen este hecho. En conjunto, los tres artículos de crítica tienen alrededor de 90 veces menos citas que el artículo original de Dunning-Kruger.  Así que parece que la mayoría de los científicos todavía piensan que el efecto Dunning-Kruger es un aspecto sólido de la psicología humana. 

Ni rastro de Dunning Kruger

El problema con el gráfico de Dunning-Kruger es que viola un principio fundamental en estadística. Si va a correlacionar dos conjuntos de datos, deben medirse de forma independiente. En el gráfico de Dunning-Kruger, este principio se viola. El gráfico mezcla la puntuación de la prueba en ambos ejes, lo que da lugar a una autocorrelación.

Al darse cuenta de este error, Edward Nuhfer y sus colegas hicieron una pregunta interesante: ¿qué sucede con el efecto Dunning-Kruger si se mide de una manera estadísticamente válida? Según la evidencia de Nuhfer, la respuesta es que el efecto desaparece.

La Figura 11 muestra sus resultados. Lo que es importante aquí es que la 'habilidad' de las personas se mide independientemente de su desempeño en las pruebas y de su autoevaluación. Para medir la 'habilidad', Nuhfer agrupa a las personas por su nivel de educación, que se muestra en el eje horizontal. El eje vertical luego traza el error en la autoevaluación de las personas. Cada punto representa a un individuo.

Figura 11: Una prueba estadísticamente válida del efecto Dunning-Kruger. Esta figura muestra la prueba del efecto Dunning-Kruger de 2017 de Nuhfer y sus colegas. Similar a la Figura 7 , este gráfico representa la habilidad de las personas frente a su error en la autoevaluación. Pero a diferencia de la Figura 7, aquí las variables son estadísticamente independientes. El eje horizontal mide la habilidad utilizando el rango académico. El eje vertical mide el error de autoevaluación de la siguiente manera. Nuhfer toma el puntaje de una persona en la prueba SLCI (prueba de inventario de conceptos de alfabetización científica) y lo resta de la autoevaluación de la persona, llamada KSSLCI (encuesta de conocimiento de la prueba SLCI). Cada punto negro indica el error de autoevaluación de un individuo. Las burbujas verdes indican las medias dentro de cada grupo, con el intervalo de confianza asociado. El hecho de que las burbujas verdes se superpongan a la línea de efecto cero indica que, dentro de cada grupo, los promedios no son estadísticamente diferentes de 0. En otras palabras, no hay evidencia de un efecto Dunning-Kruger.

Si el efecto Dunning-Kruger estuviera presente, se mostraría en la Figura 11 como una tendencia a la baja en los datos (similar a la tendencia en la Figura 7 ). Tal tendencia indicaría que las personas no calificadas sobrestiman su habilidad y que esta sobreestimación disminuye con la habilidad. Mirando la Figura 11, no hay indicios de una tendencia. En cambio, el error de evaluación promedio (indicado por las burbujas verdes) ronda el cero. En otras palabras, el sesgo de evaluación es trivialmente pequeño.

Aunque no hay indicios de un efecto Dunning-Kruger, la figura 11 muestra un patrón interesante. Moviéndose de izquierda a derecha, la dispersión del error de autoevaluación tiende a disminuir con más educación. En otras palabras, los profesores generalmente son mejores para evaluar su capacidad que los estudiantes de primer año. Eso tiene sentido. Sin embargo, tenga en cuenta que esta precisión creciente es diferente al efecto Dunning-Kruger, que se trata de un sesgo sistémico en la evaluación promedio. No existe tal sesgo en los datos de Nuhfer.

No calificado y sin saberlo

Los errores suceden. Entonces, en ese sentido, no debemos culpar a Dunning y Kruger por haberse equivocado. Sin embargo, hay una deliciosa ironía en las circunstancias de su error. Aquí hay dos profesores de la Ivy League  que argumentan que las personas no calificadas tienen una 'doble carga': las personas no calificadas no solo son 'incompetentes'... no son conscientes de su propia incompetencia.

La ironía es que la situación es en realidad al revés. En su artículo original, Dunning y Kruger son los que transmiten su incompetencia (estadística) al combinar la autocorrelación con un efecto psicológico. Bajo esta luz, el título del artículo aún puede ser apropiado. Es solo que fueron los autores (no los sujetos de prueba) quienes 'no estaban capacitados y no lo sabían'.

Blair Fix, en Economics from the Top Down El efecto Dunning-Kruger